Research
|
Producing EMRIs during SMBH binary inspirals
Production of EMRIs in Supermassive Black Hole Binaries
Authors: J. N. Bode, C. Wegg - Accepted to Monthly Notices of the Royal Astronomical Society
|
In this paper we considered the formation of extreme mass-ratio inspirals (EMRIs) sourced from a stellar cusp centered on a primary supermassive black hole (SMBH) and perturbed by an inspiraling less massive secondary SMBH. The problem was approached numerically, assuming the stars are non-interacting over these short timescales and performing an ensemble of restricted three-body integrations. From these simulations we saw that not only can EMRIs be produced during this process, but the dynamics are also quite rich. In particular, most EMRIs are produced through a process akin to the Kozai-Lidov mechanism, but with strong effects due to the non-Keplerian stellar potential, general relativity, and non-secular oscillations in the angular momentum on the orbital timescale of the binary SMBH system.
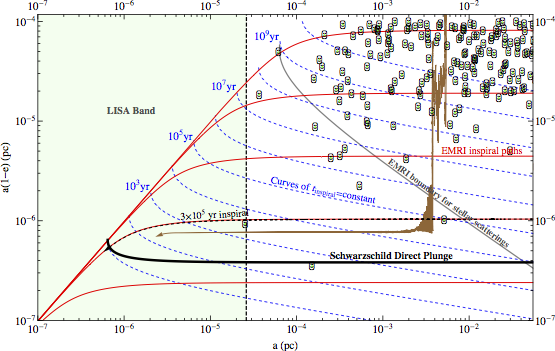
EMRI parameter space: Here we look at an example extreme mass ratio inspiral (EMRI) from our simulation (brown). A proxy for the angular momentum, a(1 − e), is plotted as a function of a where a is the semi-major axis and e is the eccentricity. A compact object (e.g., stellar-mass black hole, neutron star, white dwarf) inspirals due to gravitational wave radiation along paths shown in solid red and approximated using the standard far-field equations. The timescale for inspiral is approximately given by the times on the dashed blue curves. However, if no secondary SMBH is present and if the initial {a, a(1 − e)} pair lies above the solid gray line, the star is unlikely to complete its inspiral before two-body stellar scatterings move the orbit to larger a(1 − e). The minimum angular momentum a star can have while on a parabolic orbit without plunging into the primary SMBH, is plotted in thick solid black. The red targets are the initial conditions of a star which turned into an EMRI, the thick blue circles are the initial conditions for stars which turn into plunges, and the smiley faces are the initial conditions for stars who end the simulation uneventfully for a simulation with SMBH binary mass ratio 0.3 and stellar masses equal to 10 solar masses. As an example of a star formed from the presence of a secondary SMBH we show in solid brown the path of one of the EMRIs produced in our simulations. The star demonstrates the importance of precession due to the stellar potential and general relativity. This star has a path similar to many seen in our simulations, elucidating the new channel of EMRI production.
|
Self-Similar Solutions to the Strong Shock Problem
Slightly Two or Three Dimensional Self-Similar Solutions
Authors: R. Sari, J. N. Bode, A. Yalinewich, A. MacFadyen - Accepted to Physics of Fluids
|
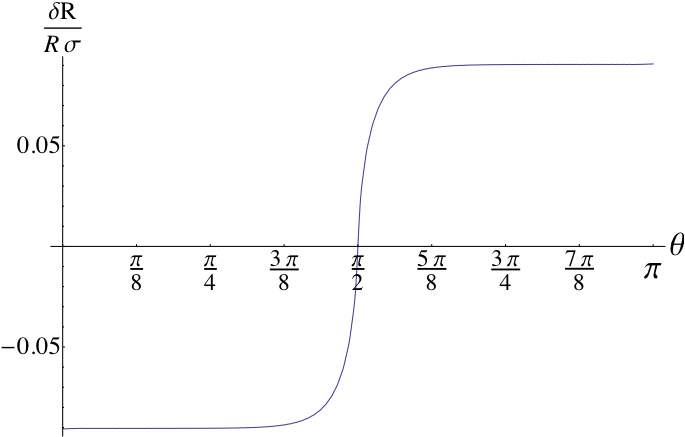
The fractional deviation of the shock position as function of θ for the heavyside density distribution. It is seen that the shock is composed of almost two hemispheres, connected smoothly over a short angular scale of about 0.2 radians.
|
Self similarity allows for analytic or semi-analytic solutions to many hydrodynamics problems. Most of these solutions are one dimensional. Using linear perturbation theory, expanded around such a one dimensional solution, we find self-similar hydrodynamic solutions that are two or three dimensional. Since the deviation from a one dimensional solution is small, we call these slightly two dimensional and slightly three dimensional self-similar solutions, respectively. As an example, we treat strong spherical explosions of the second type. A strong explosion propagates into an ideal gas with negligible temperature and density profile of the form ρ(r,θ,φ)=r^(-ω)[1+σ f(θ,φ)], with ω>3, σ << 1$. Analytical solutions are obtained by expanding the arbitrary function f(θ,φ) in spherical harmonics. We are currently waiting on simulations to check for good agreement.
|
Using Multiple Tidal Disruptions to Find Super-Massive Black Hole Binaries
Multiple Tidal Disruptions as an Indicator of Binary Super-Massive Black Hole Systems
Authors: C. Wegg and J. N. Bode - Accepted to Astrophysical Journal
|
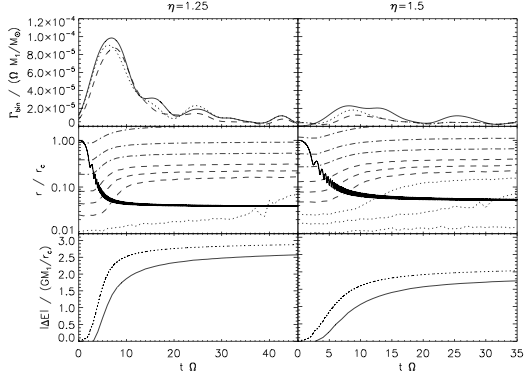
In the center row we show in dark solid the position of the secondary SMBH as a function of time, along with curves of constant interior mass. The lower row shows the consistency of our dynamical friction prescription (the two curves would be the same if our prescription were self-consistent). Finally, in the first row we show the rates of tidal disruptions on the primary over the evolution of the secondary. It is marked by an initial burst followed by a long tail. From left to right the columns are more and less numbers of stars in the central stellar cusp. We show that the rates are so high near the peak that if we were to observe two tidal disruptions from the same galaxy it is likely a super-massive black hole binary at this point in its evolution.
|
A tidal disruption is when a star gets close enough to a black hole that the difference of the force on one side of the star compared to the other is so large that the star gets torn apart. Some of the star immediately plunges into the black hole, some of the star is expelled to infinity, and the rest forms a dynamic gaseous disk around the black hole. The most likely black holes to have tidal disruptions are super-massive black holes (106-107 solar masses), which are at the centers of essentially every galaxy. When a primary super-massive black hole (SMBH) is surrounded by a significant number of stars and a secondary SMBH is inspiralling, the stars become stirred up and some fraction come close enough to the primary that they become tidally disrupted. In fact, we show that in this case (with an inspiralling secondary SMBH) the rate becomes so high that the probability of having two tidal disruptions from the same SMBH pair is so much higher than the probability of two tidal disrupations from a single SMBH, that such an occurence is an indicator of a binary system at this stage in the inspiral.
|
Electromagnetic Counterparts to Gravitational Wave Signals

Why are they important?
Electromagnetic (EM) counterparts to gravitational wave signals are interesting for multiple reasons. On one hand EM counterparts because they allow us to determine the host galaxy, something GW detectors can't do since they only give the general direction of the source galaxy. Knowing the source galaxy then lets us determine the luminosity distance-redshift relation (one of the more important relations in cosmology), which in turn gives the matter density and the dark matter equation-of-state parameter. On the other hand, because LISA indicates when the binary will merge before merger occurs, the earlier we can determine an electromagnetic counterpart the more we can watch these systems with high resolution telescopes to learn about the dynamics. It is very rare in astrophysics that we can watch dynamical systems well enough to learn about the objects involved.
Introduction to the problem we consider:
It is currently believed that most galaxies harbor super-massive black holes (SMBHs) in their cores. When a galaxy undergoes a merger the lowest mass SMBH will begin an inspiral due to dynamical friction into the core of the larger galaxy. Dynamical friction carries this black hole until around one parsec from the primary (larger) SMBH, at which point a process not yet entirely understood carries the secondary (smaller) SMBH to a point that gravitation wave (GW) emission dominates the inspiral until merger.
If there is gas present, the binary will, through quadrupolar torques on the disk, align partially aligned disks with the orbital angular momentum of the binary. At the same time the gas being accreted onto both will act to align the spins of the individual SMBHs with the orbital angular momentum of the disk. When the binary becomes sufficiently tight the torques the binary exerts on the disk are enough to overcome the viscous losses of the disk, which effectively evacuates the inner region of the disk (the binary "pushes" material outwards).
The inner disk settles into a steady state situation with an inner edge at approximately twice the binary separation. While the viscous timescales are short compared to the merger time (time to merger) the disk will follow the binary inwards as the binary loses angular momentum due to GW emission. When the viscous time becomes longer than the merger time the binary disengages from the disk (stops exerting torques), and the disk begins an infall on a viscous timescale.
Because the binary inspirals faster than the disk can fall inwards, when merger occurs the disk will not have evolved significantly. This will leave the merger surrounded by an axisymmetric disk with an evacuated inner region.
|
Analytic Solution to the Response of a Circumbinary Disk Following SMBH Mergers
Authors: E. Sterl Phinney & J. Nate Bode, in prep.
|
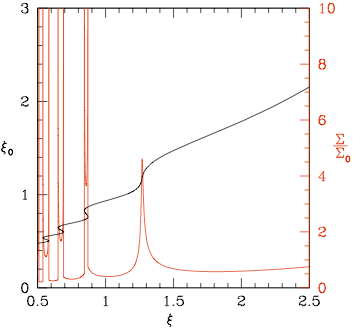
On the left y-axis (black) we plot the initial position of noninteracting particles against their final positions on the x-axis. On the right y-axis (red) we plot the surface density over initial surface density as a function of position in the disk. Where multiple particles end up at the same final position caustics have formed (visible by their characteristic double peaks). In this case the first caustic defines the boundary of the region of relevance for our analytic solution, and a shock is expected in its location.
|
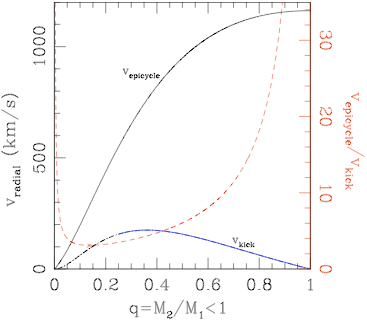
In blue we plot the kick velocity due to gravitational wave recoil for non-spinning black holes. In solid black we plot the disk radial velocity (v_epicycle) due to the mass loss. The ratio of the disk radial velocity to the kick velocity (shown in red dashed with the right y-axis) determines the relative importance of mass loss and kicks to the inner disk. Where this ratio is greater than 1 the mass loss is more important than kicks.
|
Since we are assuming that there is a gaseous disk one would expect the gas to have interacted with both SMBHs and acted to align their spins somewhat with the angular momentum of the disk. This reduces the probability of superkicks during merger. We do a literature search of many of the GR simulations of black hole mergers with spins aligned or antialigned with the binary's orbital angular momentum and compare the importance of mass loss to the disk's evolution to the importance of kicks. We show that for almost all sets of parameters for black holes aligned and anti-aligned with the disk (but with varying mass ratio and spin) the mass loss is more important than kicks to the disk response.
In the noninteracting limit we solve for the reaction of the gaseous disk and produce an analytic solution for the surface density as a function of time. We describe the region of relevance of this solution and show that it is almost always bounded by shocks. The Mach numbers of these shock(s) can be reasonably approximated (to within ~10%) using our analytic solution. Because shortly following the shocks the disk circularizes, our solution quantitatively characterizes most observables of the system, since it not only describes the flow prior to the shocks, but also describes the strength of the shocks. Using two parameters which we introduce (the epicyclic Mach number and the relative energy) and our analytic machinery we can determine the flows prior to the formation of the first shocks, the Mach number of the first (and strongest) shocks, and therefore have a good idea of the observable effects mass loss and kicks have on the disk.
|
Relevant Talks & Posters:
♦ Variability in Circumbinary Disks Following Massive Black Hole Mergers, Poster presented at the APS April Meeting in 2007.
♦ Simulations of Circumbinary Disks Following Massive Black Hole Mergers, Talk given at the Theoretical Astrophysics in Southern California meeting at UCLA in 2007.
|
1D Simulations of Circumbinary Disk Response Following SMBH Mergers
Authors: J. Nate Bode & E. Sterl Phinney; Journal: in prep.
|
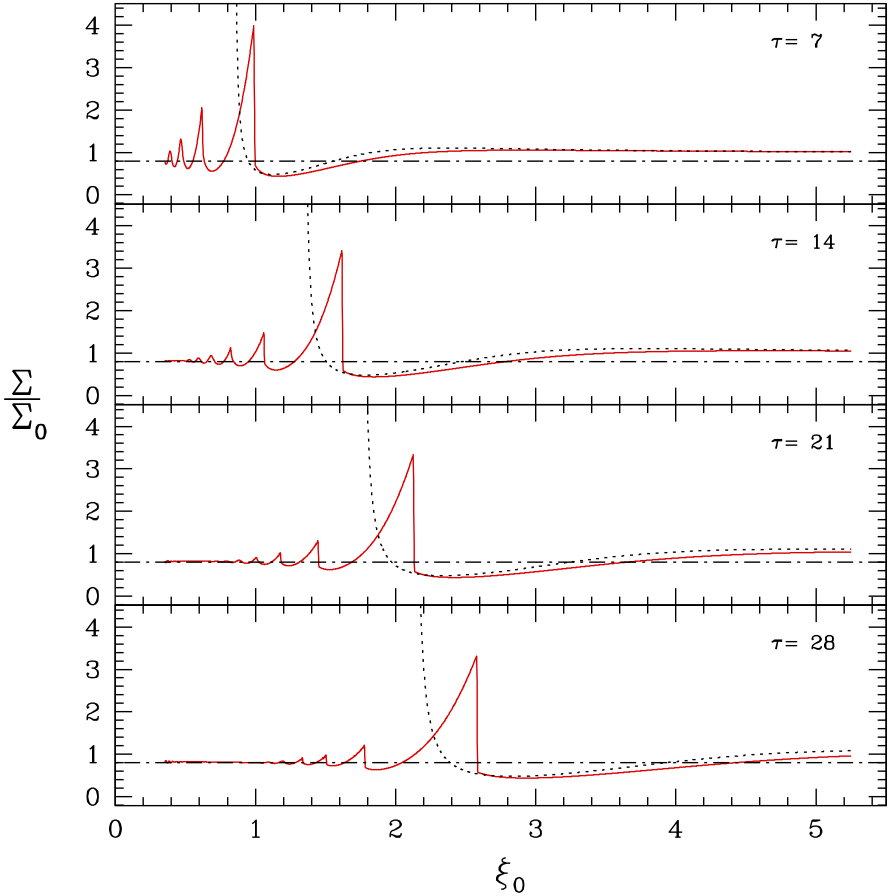
We plot the normalized surface density as a function of the initial coordinates of the fluid elements (i.e. Lagrangian coordinates) using our 1D simulation in solid red and show the analytic solution until the formation of the first caustic in dotted black. A strong shock is expected just prior to the first caustic (as is visible here). The epicyclic contractions feed energy into the shock and ensure that the shock always remains slightly in advance of the caustic. This allows for a lower bound of the Mach number of the shock. In dash-dot (black) we also plot the theoretical final surface density derived using conservation of specific angular momentum.
|
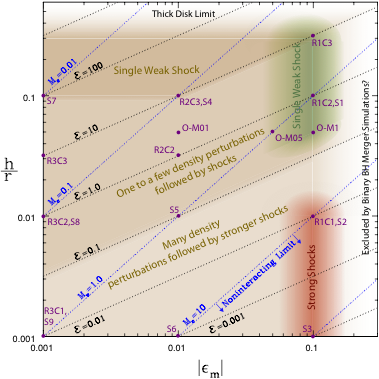
The disk response as a function of the independent variables: the local scale height over r, h/r, and the mass perturbation, epsilon_m. The dependent variables, the relative energy (script E) and the epicyclic Mach number (M_e), are also shown. Brief descriptions of the different flows are labeled and color coded. Simulations discussed in the paper are given by the maroon labels.
|
We follow up paper 1 with a simulation paper where we use a 1D hydrodynamic simulation to consider mergers with only mass loss (something we showed in paper 1 was a good approximation). Our simulation is a standard 1D Lagrangian finite-differencing leapfrog method using a von Neumann-Richmyer artificial viscosity. Because of the efficiency of the code we can easily span the entirety of allowed parameter space. Running some forteen simulations we show that the solution of paper 1 is indeed accurate, and characterize all possible disk responses using the epicyclic Mach number and the relative energy (the two parameters we introduced in paper 1). This is demonstrated graphically in a summary figure (shown to the left) plotting all possible flows in parameter space.
There are several timescales to consider in our solution: the caustic formation time, the shock formation time, and the time when the flow will deviate from our analytic solution. The deviation time approaches the caustic formation time in the limit of either large mass perturbations or very thin disks, but can also be as short as the time until the first epicyclic overdensity in the case of thicker disks. These thicker disks will invariably form shocks in the region just following where the flow deviates from our analytic solution, though the formation time ranges from almost instantaneous to quite long. We discuss these timescales and describe how to use them to predict different types of flows and the strength of the shocks.
The strength of the shocks can be well approximated. This is straight forward since one important characteristic of the shocks is that they remain more or less stationary with respect to the analytic solution, as can be seen in the upper figure to the left. This occurs because the epicyclic motion is constantly injecting energy into the shock ensuring that it remains moving at least as fast as the "analytic" flow which precedes it. Using the local sound speed and the speed of the density peaks of the analytic solution one may easily calculate a lower bound to the Mach number of the shock and therefore have a good understanding of the shock heating which will be occurring.
A succinct but thorough description of how to use the epicyclic Mach number and the relative energy to determine the disk response is provided and the method is used on the example of the 3D MHD simulations of O'Neill et.al. 2009 . Our analytic method and simulation describe to ~10% their emissions, a remarkable feat for a method requiring only moderate calculations.
|
Relevant Talks & Posters:
♦ Circumbinary Disks Following SMBH Mergers, Talk given at the 8th International LISA Symposium in June 2010.
♦ Observability of Circumbinary Disks Following Massive Black Hole Mergers, Poster presented at the 213th AAS Meeting (Long Beach, Ca) in Jan 2009.
|
|
Last updated: June 16, 2015
|